Marta Macho Stadler, autora de ‘Matemáticas y Literatura’: Tres incursiones de los números en el mundo de las letras

El Cuervo es uno de los poemas más conocidos de Edgar Allan Poe y el propio autor reconoció “que ningún detalle de su composición puede asignarse al azar o una intuición, sino que la obra se desenvolvió paso a paso hasta quedar completa con la precisión y rigor lógico de un problema matemático”.

Con esta cita arranca el libro Matemáticas y Literatura (Catarata) de Marta Macho Stadler, profesora de Topología en la Universidad del País Vasco y una de las responsables del portal DivulgaMAT, quien apunta: “La mayoría de la gente percibe a las matemáticas como algo mecánico y falto de imaginación, y que la creación literaria es el resultado de grandes dosis de arte e inspiración, pero ni lo uno ni lo otro se adecúan a la realidad”.

“Las matemáticas germinan como una combinación de novedosas ideas, instinto y la técnica propia del oficio científico –subraya–, y el texto literario resulta de una cuidada planificación y del buen hacer de la persona que escribe”.

Su libro contiene fragmentos de obras en los que se muestra cómo la literatura se inspira en las matemáticas, y cómo la estructura o el contenido de poemas o novelas también pueden impulsar conjeturas y teoremas matemáticos. “Uniendo matemáticas y textos literarios se puede leer para disfrutar y aprender”, comenta la autora. Estos son tres ejemplos.

1. El ritual de los Musgrave (Arthur Conan Doyle)

Huella matemática en extractos literarios

Este relato está protagonizado por el famoso detective Sherlock Holmes, quien debe aclarar la desaparición del mayordomo de la familia Musgrave, al que sorprendieron fisgando unos papeles en la biblioteca. En concreto, estaba leyendo un antiguo documento sobre la localización de un misterioso objeto:

[…] -¿Dónde estaba el sol?

-Sobre el roble.

-¿Dónde estaba la sombra?

-Bajo el olmo.

-¿Con qué pasos se medía?

-Al norte por diez y por diez, al este por cinco y por cinco, al sur por dos y por dos, al oeste por uno y por uno, y por debajo. […]

Del viejo olmo solo queda su tocón en el jardín de la familia, pero se conocía su altura, y permanece el gigantesco roble. Cuando el sol roza su copa, Holmes observa su sombra y mide la que proyecta un pequeño triángulo que ha formado con una caña de pescar y un cordel.

Aplicando el teorema de proporcionalidad de triángulos de Tales [si en un triángulo se traza una línea paralela a cualquiera de los lados, se obtiene un triángulo dado], el detective logra encontrar el punto definido por la sombra del olmo.

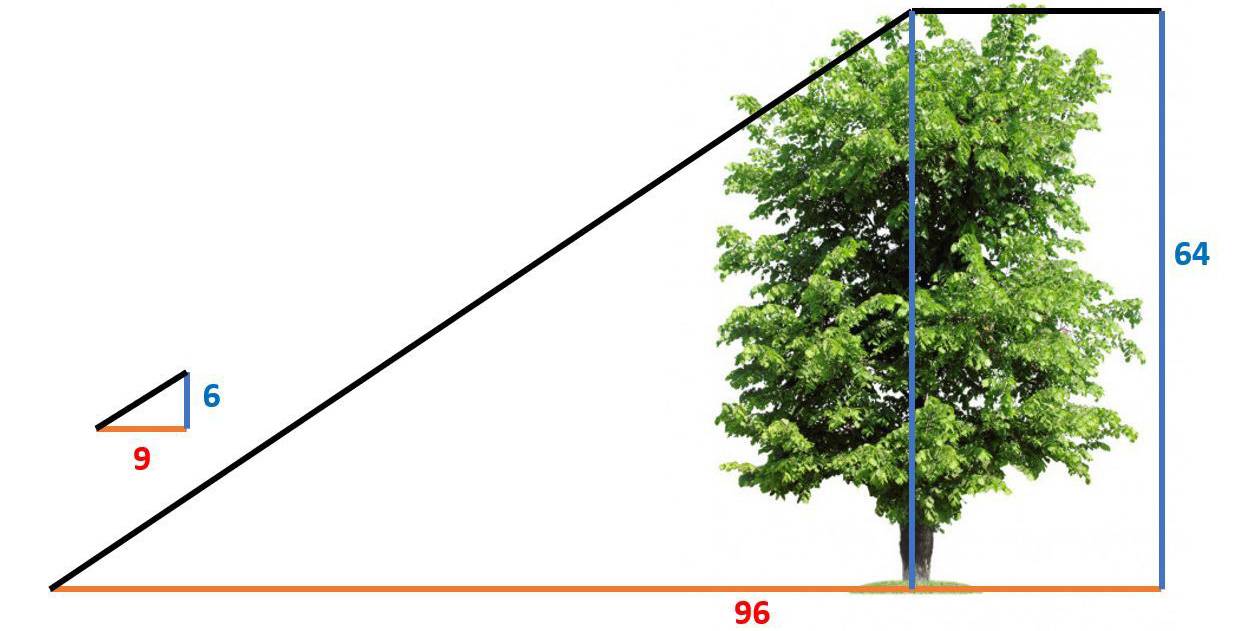
Sherlock Holmes aplicó el teorema de proporcionalidad de triángulos de Tales para resolver este caso. / Marta Macho Stadler

Tras resolver este problema y realizar los últimos cálculos que indicaba el documento, Holmes descubre así el paradero del mayordomo, además de un antiguo secreto de la familia Musgrave relacionado con la monarquía británica.

2. Un poema sobre la banda de Möbius (Luc Étienne)

Escribiendo bajo traba matemática

La banda de Möbius es una superficie –tiene dimensión 2– que sin embargo presenta una sola cara y no es orientable. El escritor francés Luc Étienne aprovechó las propiedades de este objeto geométrico para cambiar el significado de un poema estructurado en dos partes.

El punto de partida es una tira de papel donde en una de sus caras se escribe este cuarteto:

Trabajar, trabajar sin cesar,

para mi es una obligación

no puedo flaquear

pues amo mi profesión…

A continuación se gira la cinta de papel, sobre su lado más largo, y se pone la segunda mitad:

Es realmente un tostón

perder el tiempo,

y grande es mi sufrimiento,

cuando estoy de vacación.

El significado de un poema formado por dos cuartetos escritos en las dos caras de una misma tira (aunque separados aquí en dos para su mejor visualización), cambia al convertirla en una banda de Möbius. / Marta Macho Stadler

Después se pega la tira para formar una banda de Möbius, y el poema, inicialmente escrito sobre dos caras, aparece ahora solo en una, cambiando totalmente el sentido de la poesía. Lo que era una alabanza al esfuerzo y al trabajo se convierte en un elogio a la holgazanería:

Trabajar, trabajar sin cesar, es realmente un tostón

para mi es obligación perder el tiempo

no puedo flaquear y grande es mi sufrimiento,

pues amo mi profesión… cuando estoy de vacación.

3. La historia de Plattner (H. G. Wells)

Matemáticas como hilo conductor

En su conocida novela de ciencia ficción La máquina del tiempo, Herbert George Wells habla de la cuarta dimensión, entendida como la magnitud física del tiempo. Un año después de su publicación, el escritor británico presentó La historia de Plattner, donde aparece de nuevo ese concepto, pero esta vez con un significado matemático: mundos de cuatro dimensiones.

Como seres que vivimos en dimensión 3, no podemos imaginar o visualizar las dimensiones ‘extra’ más que proyectando sus objetos en 3D desde diferentes lados, como ocurre con el teseracto (un cubo de dimensión 4). En cualquier caso, suceden cosas muy extrañas en la cuarta dimensión.

En esta historia, Plattner es un profesor que desaparece, ante sus atónitos alumnos, tras una explosión provocada durante un experimento de química. Durante los nueve días en los que permanece ausente, el docente aparece, como si fuera un espectro, en los sueños de algunos de sus vecinos. Regresa de manera súbita, cayendo de algún lugar, sin poder aclarar lo sucedido.

Pero sorprendentemente su cuerpo se ha transformado: sus partes derecha e izquierda han cambiado de lugar. Y esto solo es posible si ha viajado a la cuarta dimensión, como explica el propio Wells, por analogía con lo que ocurre al pasar de la dimensión 2 a la 3: “Si se recorta una figura de papel, cualquier figura con un lado derecho y otro izquierdo, se puede cambiar su forma invirtiéndola”. Por ejemplo, para invertir una figura plana, como una cara, es preciso hacerlo en el espacio tridimensional, no se puede en el bidimensional.

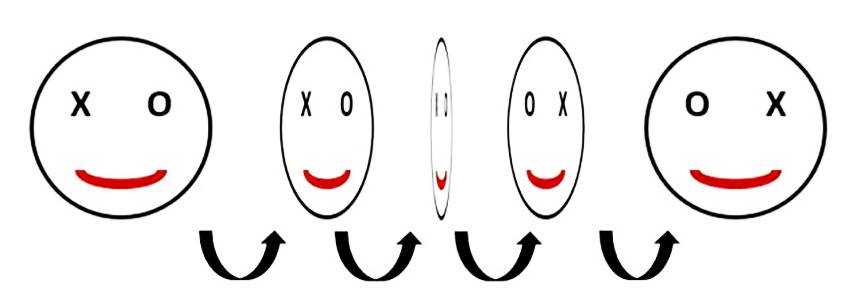
Explicación de cómo se invierte un objeto de dimensión 2 en el espacio tridimensional para entender lo que le sucede a Plattner. / Marta Macho Stadler

“Pero con un cuerpo sólido [con tres dimensiones] es diferente –continúa Wells–. Los matemáticos nos dicen que la única manera de cambiar sus lados derecho e izquierdo es sacarle del espacio que conocemos, sustraerlo de la existencia ordinaria y llevarle a cualquier otro espacio exterior. […] Para expresarlo en un lenguaje técnico, la curiosa inversión de los lados derecho e izquierdo de Plattner es una prueba de que ha escapado de nuestro espacio hacia el que recibe el nombre de cuarta dimensión, y que después ha regresado a nuestro mundo”.